三点构成圆

发表于 2020-07-21 分类于数学，线性代数与几何，计算几何阅读次数： Valine：

三点构成圆

阅读全文 »

判断一个点是否在一个四面体内部

发表于 2020-07-21 分类于数学，线性代数与几何，计算几何阅读次数： Valine：

判断一个点是否在一个四面体内部

体积法

阅读全文 »

重心坐标插值

发表于 2020-07-21 更新于 2020-07-21 分类于数学，线性代数与几何，计算几何阅读次数： Valine：

重心坐标插值(Barycentric Interpolation)

用来插值

线段的重心坐标插值

$P=tA+(1-t)B$

三角形重心坐标插值

点$P$在$\triangle ABC$组成的三角形内

求点$P$的重心坐标插值$(\alpha,\beta,\gamma)$

$P=\alpha A+\beta B+\gamma C$ $\alpha+\beta+\gamma = 1$

面积

$S_{\triangle ABC} = \alpha S_{\triangle PBC} + \beta S_{\triangle PAC} + \gamma S_{\triangle PAB}$

三角形的重心坐标 $\alpha = \beta = \gamma = 1 / 3$

$P=\frac{1}{3} A+\frac{1}{3} B+\frac{1}{3} C$

三维四面体的重心坐标插值

四面体的重心坐标
$P_{center} = \frac {P_1+P_2+P_3+P_4} {4}$
求点$P$的重心坐标插值$(\alpha,\beta,\gamma,\delta)$
$\alpha+\beta+\gamma+\delta = 1$ $P = \alpha A+\beta B+\gamma C+\delta D$
体积
$V_{\square ABCD} = \alpha V_{\square PBCD} + \beta V_{\square PACD} + \gamma V_{\square PABD} + \delta V_{\square PABC}$
点P是否在四面体内部

阅读全文 »

三角形的外接圆

发表于 2020-07-21 分类于数学，线性代数与几何，计算几何阅读次数： Valine：

三角形的内切圆

发表于 2020-07-21 分类于数学，线性代数与几何，计算几何阅读次数： Valine：

三角形的法线

发表于 2020-07-20 更新于 2020-07-21 分类于数学，线性代数与几何，计算几何阅读次数： Valine：

已知三角形三点，三角形的法线方向

已知点P组成的所有三角形的法线，点P的法线

已知三点的法线，三角形内部点P的法线插值

阅读全文 »

三角形裁剪

发表于 2020-07-20 分类于数学，线性代数与几何，计算几何阅读次数： Valine：

三角形裁剪

阅读全文 »

三角形插值

发表于 2020-07-20 更新于 2020-07-21 分类于数学，线性代数与几何，计算几何阅读次数： Valine：

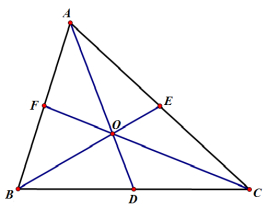
三角形插值(重心坐标)

点$P$在$\triangle ABC$组成的三角形内

求点$P$的插值$\alpha,\beta,\gamma$

先求出$\vec{AP}$与$\vec{BC}$的交点$A^,$

然后计算$\alpha,\beta,\gamma$

float* lt::InterpolationTriangle(Vector2<float> p, Vector2<float> a, Vector2<float> b, Vector2<float> c)
{
	Vector2<float> a1b1 = p - a;
	Vector2<float> a2b2 = c - b;
	Vector2<float> a2a1 = a - b;
	Vector2<float> a1a2 = b - a;
	float u = (a2b2.x * a2a1.y - a2a1.x * a2b2.y) / (a1b1.x * a2b2.y - a2b2.x * a1b1.y);
	Vector2<float> aintersected = a + a1b1 * u;

	float arr[3];
	arr[0] = (p - a).magnitude() / (aintersected - a).magnitude();
	arr[1] = (aintersected - p).magnitude() / (aintersected - a).magnitude() * (aintersected - b).magnitude() / (c-b).magnitude();
	arr[2] = (aintersected - p).magnitude() / (aintersected - a).magnitude() * (c - aintersected).magnitude() / (c - b).magnitude();
	return arr;
}