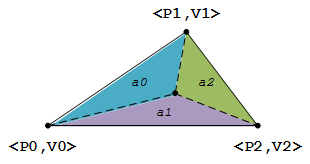
三角形插值(重心坐标)

点$P$在$\triangle ABC$组成的三角形内

求点$P$的插值$\alpha,\beta,\gamma$

先求出$\vec{AP}$与$\vec{BC}$的交点$A^,$

然后计算$\alpha,\beta,\gamma$

float* lt::InterpolationTriangle(Vector2<float> p, Vector2<float> a, Vector2<float> b, Vector2<float> c)
{
	Vector2<float> a1b1 = p - a;
	Vector2<float> a2b2 = c - b;
	Vector2<float> a2a1 = a - b;
	Vector2<float> a1a2 = b - a;
	float u = (a2b2.x * a2a1.y - a2a1.x * a2b2.y) / (a1b1.x * a2b2.y - a2b2.x * a1b1.y);
	Vector2<float> aintersected = a + a1b1 * u;

	float arr[3];
	arr[0] = (p - a).magnitude() / (aintersected - a).magnitude();
	arr[1] = (aintersected - p).magnitude() / (aintersected - a).magnitude() * (aintersected - b).magnitude() / (c-b).magnitude();
	arr[2] = (aintersected - p).magnitude() / (aintersected - a).magnitude() * (c - aintersected).magnitude() / (c - b).magnitude();
	return arr;
}

重心法(质心)

显然，无论是线性插值还是双线性插值的都无法解决这个问题。而使用重心坐标则可以很好的解决这个问题。简单的来说，重心坐标就是子三角形与大三角形的面积比，具体的解释参看维基百科，计算过程如下：

　　已知三角形的三个顶点坐标P1, P2, P3, 在三角形内的任意点P, 都存在u和v（由于三角形是一个2D图形，只有两个自由度，所以只要u和v即可）,使得

　　　　P = (1 - u - v) P1 + u P2 + v * P3

　　P点在三角形内，所以(u, v)必须满足条件u ≥ 0, v ≥ 0, u + v ≤ 1。u、v体现了每个顶点对特定区域的权重贡献，(1 - u - v)则是第三个权重，只要计算出u和v，就可以计算出每个顶点对P点的贡献。现在已知P1, P2, P3和P的坐标值，求解u和v，只需要解二元一次方程即可：

　　　　P.x = (1 - u - v) P1.x + u P2.x + v * P3.x

　　　　P.y = (1 - u - v) P1.y + u P2.y + v * P3.y

　　有了u、v值，对P1, P2, P3的颜色值进行加权平均，即可得到P点颜色值。

float* lt::InterpolationTriangle(Vector2<float> p, Vector2<float> a, Vector2<float> b, Vector2<float> c) {
	float arr[3];
	arr[1] = ((p.x - a.x)*(c.y - a.y) - (c.x - a.x) * (p.y - a.y)) / ((b.x - a.x) * (c.y - a.y) - (c.x - a.x) * (b.y - a.y));
	arr[2] = ((p.x - a.x)*(b.y - a.y) - (b.x - a.x) * (p.y - a.y)) / ((c.x - a.x) * (b.y - a.y) - (b.x - a.x) * (c.y - a.y));
	arr[0] = 1 - arr[1] - arr[2];
	return arr;
}

面积法

a0 占三角形整体面积的比例代表 V2(P2对应的数值)占 V 的比例,
a1 占三角形整体面积的比例代表 V1(P1对应的数值)占 V 的比例,
而 a2 占三角形整体面积的比例则代表 V0(P0对应的数值)占 V 的比例,

public static float Cross(Vector2 v0, Vector2 v1)
{
    return v0.x * v1.y - v1.x * v0.y;
}

public static float TriangleArea(Vector2 v0, Vector2 v1)
{
    return 0.5f * Math.Abs(Cross(v0, v1));
}

public static float TriangleLerp(Value2f val0, Value2f val1, Value2f val2, Vector2 p)
{
    var v01 = val1.Vector - val0.Vector;
    var v02 = val2.Vector - val0.Vector;
    var v0p = p - val0.Vector;

    var a = TriangleArea(v01, v02);
    Debug.Assert(a > 0, "[MathUtil]Error to do triangle Lerp, seems vertexes collinear ...");

    var a0 = TriangleArea(v01, v0p);
    var a1 = TriangleArea(v0p, v02);
    var a2 = a - a0 - a1;

    return (val2.v * a0 + val1.v * a1 + val0.v * a2) / a;
}