鸡蛋掉落
问题描述
你将获得 K 个鸡蛋,并可以使用一栋从 1 到 N 共有 N 层楼的建筑。
每个蛋的功能都是一样的,如果一个蛋碎了,你就不能再把它掉下去。
你知道存在楼层 F ,满足 0 <= F <= N 任何从高于 F 的楼层落下的鸡蛋都会碎,从 F 楼层或比它低的楼层落下的鸡蛋都不会破。
每次移动,你可以取一个鸡蛋(如果你有完整的鸡蛋)并把它从任一楼层 X 扔下(满足 1 <= X <= N)。
你的目标是确切地知道 F 的值是多少。
无论 F 的初始值如何,你确定 F 的值的最小移动次数是多少?
动态规划
问题分析
f(i,j) i 代表鸡蛋个数,j代表楼层
f(i,j)=min(max(f(i,f-1) + 1,f(i-1,j-f)+1)) i<=f<=j
| i\j |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 2 |
1 |
2 |
2 |
3 |
3 |
3 |
4 |
4 |
4 |
| 3 |
1 |
2 |
2 |
3 |
3 |
3 |
3 |
4 |
4 |
| 4 |
1 |
2 |
2 |
3 |
3 |
3 |
3 |
4 |
4 |
| 5 |
1 |
2 |
2 |
3 |
3 |
3 |
3 |
4 |
4 |
| 9 |
1 |
2 |
2 |
3 |
3 |
3 |
3 |
4 |
4 |
O(KNN)
超时
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution {
public:
int dp[101][1001] = { 0 };
int superEggDrop(int K, int N) {
int i, j, f;
for (i = 1; i <= K; i++)
{
dp[i][1] = 1;
}
for (j = 1; j <= N; j++)
{
dp[1][j] = j;
}
int temp;
for (i = 2; i <= K; i++)
{
for (j = 2; j <= N; j++)
{
dp[i][j] = max(dp[i - 1][0] + 1, dp[i][j - 1] + 1);
for (f = 2; f <= j; f++)
{
temp = max(dp[i - 1][f - 1] + 1, dp[i][j - f] + 1);
dp[i][j] = min(dp[i][j], temp);
}
}
}
return dp[K][N];
}
};
|
动态规划+二分法
问题分析
max(dp[i - 1][fMedian - 1] + 1, dp[i][j - fMedian] + 1)函数是一个先递减在递增或者先递增再递减的函数,并且导数比较稳定
超时
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
| class Solution {
public:
int dp[101][10001] = {0};
int superEggDrop(int K, int N) {
int i, j;
for (i = 1; i <= K; i++)
{
dp[i][1] = 1;
}
for (j = 1; j <= N; j++)
{
dp[1][j] = j;
}
int temp;
int ff;
int fMin, fMax;
int fMedian;
int median,left, right;
int ii, jj;
for (i = 2; i <= K; i++)
{
for (j = 2; j <= N; j++)
{
fMin = 1; fMax = j;
while (fMin <= fMax)
{
fMedian = (fMin + fMax) / 2;
median = max(dp[i - 1][fMedian - 1] + 1, dp[i][j - fMedian] + 1);
if (fMedian == 1)
{
for (ii = fMedian + 1; ii <= j; ii++)
{
right = max(dp[i - 1][ii - 1] + 1, dp[i][j - ii] + 1);
if (right != median)
{
break;
}
}
if (median >= right)
{
fMin = fMedian + 1;
}
else
{
break;
}
}
else if (fMedian == j)
{
for (jj = fMedian - 1; jj >= 1; jj--)
{
left = max(dp[i - 1][jj - 1] + 1, dp[i][j - jj] + 1);
if (left != median)
{
break;
}
}
if (median >= left)
{
fMax = fMedian - 1;
}
else
{
break;
}
}
else
{
for (ii = fMedian + 1; ii <= j; ii++)
{
right = max(dp[i - 1][ii - 1] + 1, dp[i][j - ii] + 1);
if (right != median)
{
break;
}
}
if (median >= right)
{
fMin = fMedian + 1;
continue;
}
for (jj = fMedian - 1; jj >= 1; jj--)
{
left = max(dp[i - 1][jj - 1] + 1, dp[i][j - jj] + 1);
if (left != median)
{
break;
}
}
if (median >= left)
{
fMax = fMedian - 1;
continue;
}
break;
}
}
dp[i][j] = median;
}
}
return dp[K][N];
}
};
|
动态规划+二分法
问题分析
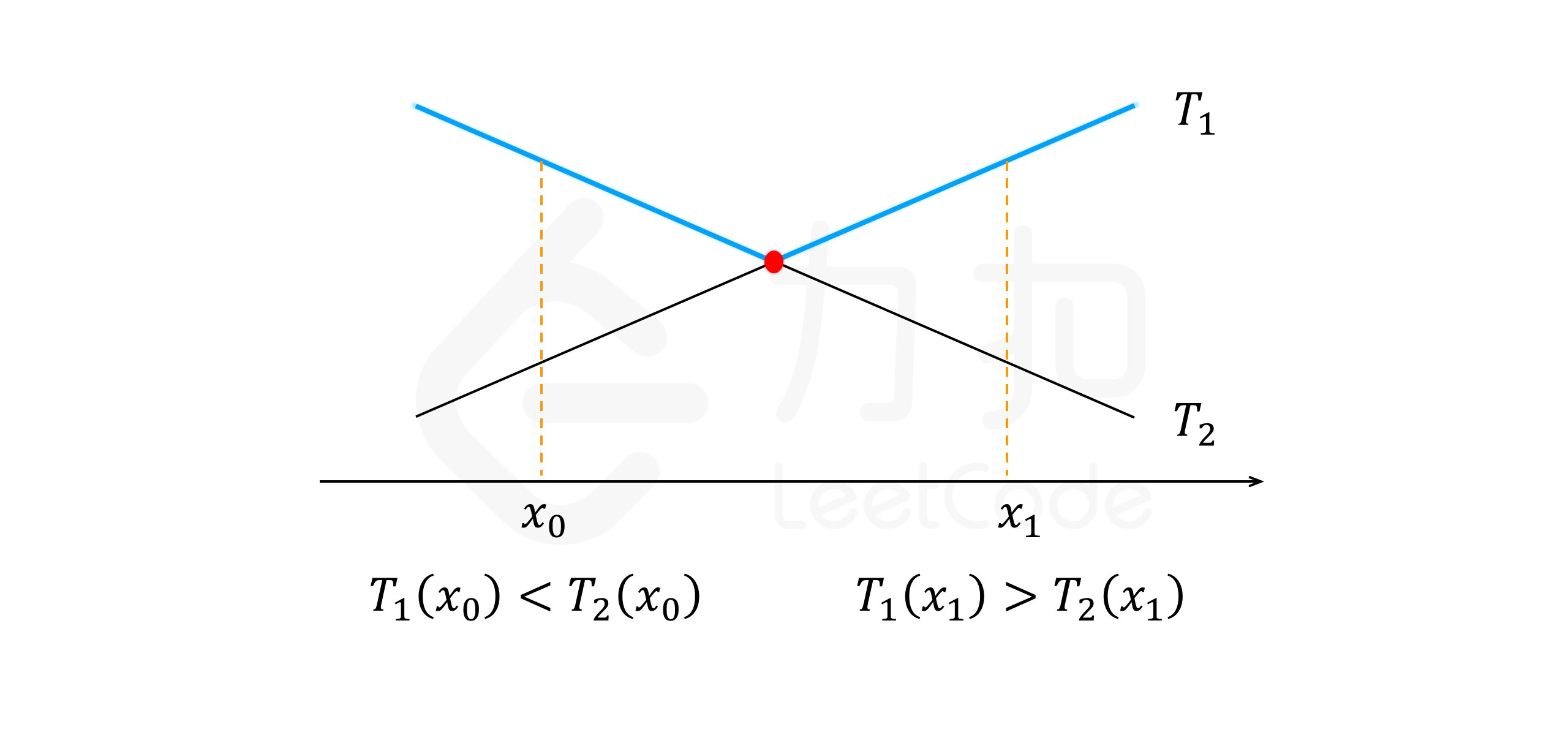
图片来源于leetcode
fMedian 的计算二分查找
- 1.T1 = dp[i - 1][f - 1] 是单调递增函数
- 2.T2 = dp[i][j - f] 是单调递减函数
- 3.max(dp[i - 1][f - 1],dp[i][j - f]),就是两个函数的交点
- 4.交点可能是浮点数,如果是整数,fmin=fmax=fmedian 如果是浮点数,离散化,求出交点位置的左右点
完美解决问题
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| class Solution {
public:
int dp[101][10001] = {0};
int superEggDrop(int K, int N) {
int i, j;
for (i = 1; i <= K; i++)
{
dp[i][1] = 1;
}
for (j = 1; j <= N; j++)
{
dp[1][j] = j;
}
int temp;
int ff;
int fMin, fMax;
int fMedian;
int median,left, right;
int ii, jj;
for (i = 2; i <= K; i++)
{
for (j = 2; j <= N; j++)
{
fMin = 1; fMax = j;
while (fMin + 1 < fMax)
{
fMedian = (fMin + fMax) / 2;
left = dp[i - 1][fMedian - 1];
right = dp[i][j - fMedian];
if (left < right)
{
fMin = fMedian + 1;
}
else if (left > right)
{
fMax = fMedian - 1;
}
else
{
fMin = fMedian;
fMax = fMedian;
}
}
median = min(max(dp[i - 1][fMin - 1] + 1, dp[i][j - fMin] + 1)
, max(dp[i - 1][fMax - 1] + 1, dp[i][j - fMax] + 1));
dp[i][j] = median;
}
}
return dp[K][N];
}
};
|
