矩阵连乘

问题描述

---

给定n个矩阵｛A1,A2,…,An｝，其中，Ai与Ai+1是可乘的，(i=1,2 ,…,n-1)。用加括号的方法表示矩阵连乘的次序，不同的计算次序计算量（乘法次数）是不同的，找出一种加括号的方法，使得矩阵连乘的次数最小。

例如：

 A1是A（5*10）的方阵；

 A2是A（10*100）的方阵；

 A3是A（100*2）的方阵；

那么有两种加括号的方法：

  1. （A1A2）A3；
  2.   A1（A2A3）；

  第一种方法的计算量：5*10*100+5*100*2=6000；

  第二种方法的计算量：10*100*2+5*10*2=2100；  

---

问题分析

---

递归性质：

• 1.两个矩阵相乘的次数 A(x1,y1) A(x2,y2) 的相乘次数等于 x1 y1 y2;(y1 = x2)
• 2.f(i,j) = min(f(i,k)+f(k+1,j) + Ai.x Ak.y Aj.y) (i<=k<j)
• 3.主要特征f(i,j) 取决于 f(i,k)和f(k+1,j) 也就是f(i,j)取决于i行前面的数据和j列后面的数据

---

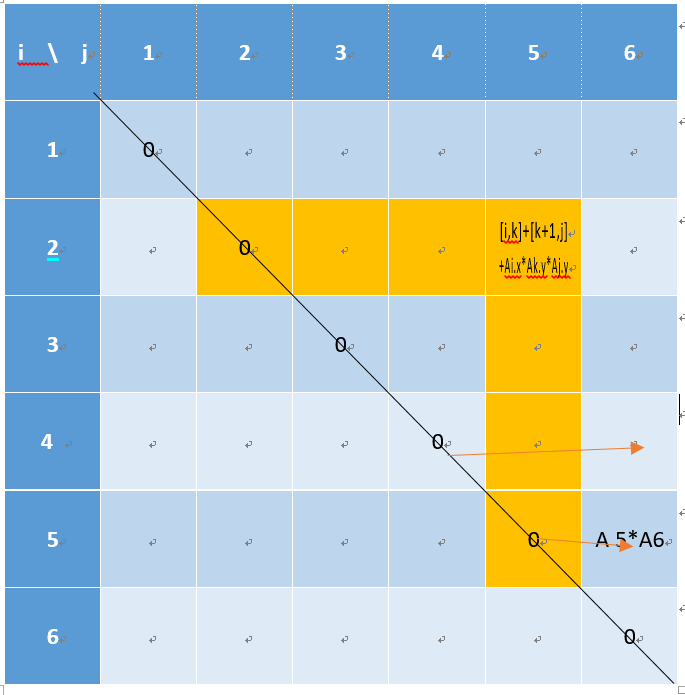
动态规划对角线

---

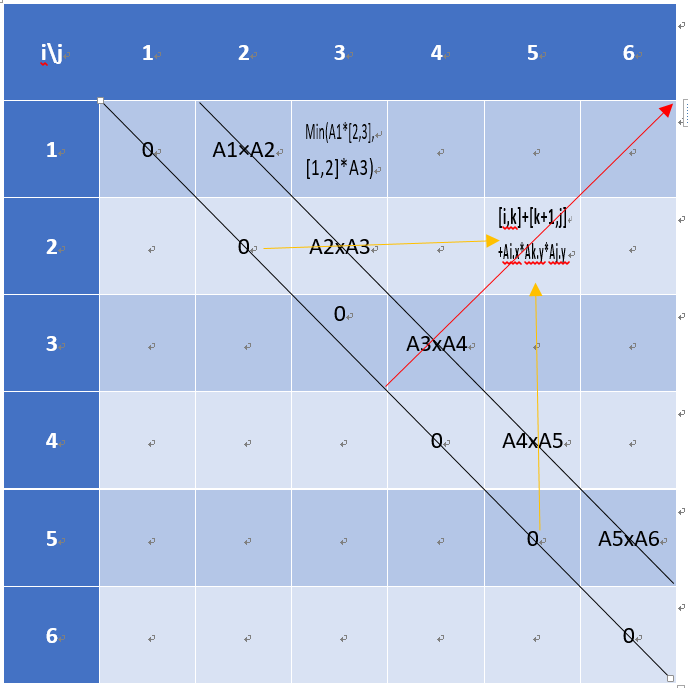
先计算对角线，再计算次对角线，依次向右上角推进
dp[i][j] = min(dp[i,k]+dp[k+1,j]+Ai.xAk.yAj.y

for(int d = 1;d<=n;d++)
{
  for(int i = 0; i < n; i ++)
  {
    int j = i + d;
    for(int k = i; k <= j; k ++)
    {
      dp[i][j] = Min(dp[i][j],dp[i][k]+dp[k+1][j] + A[i].x * A[k].y * A[j].y);
    }
  }
}

或者

for(int j = 1;j<=n;j++)
{
  for(int i = 0; i < n; i ++)
  {
    for(int k = i; k <= i + j; k ++)
    {
      dp[i][i + j] = Min(dp[i][i + j],dp[i][k]+dp[k+1][i + j] + A[i].x * A[k].y * A[i + j].y);
    }
  }
}

---

动态规划行式

---

依次计算 n n-1 n-2 … 2 1 行，即可求得右上角

dp[i][j] = min(dp[i,k]+dp[k+1,j]+Ai.xAk.yAj.y

for(int i = n-1;i >= 0; i ++)
{
  for(int j = i+1;j < n; j++)
  {
    for(int k = i; k < j; k ++)
    {
      dp[i][j] = Min(dp[i][j],dp[i][k] + dp[k+1][j] + A[i].x * A[k].y * A[j].y);
    }
  }
}

---