开方算法

开方算法依据公式

开平方公式
(a+b)²-a²=b(2a+b)
开立方公式
(a+b)³-a³=b(3a²+3ab+b²)

1.开方作法本原图
2.二项式定理

1.竖式开方法
2.迭代求根法
3.二分法

牛顿迭代法

迭代公式: t = (t+x/t)/2.0

1
2
3
4
5
6
7
8

double sqrt(double x) {
  double eps = 1e-12;
  double t = x;
  while (abs(t - x / t) > eps * t) {
    t = (t + x / t) / 2.0;
  }
  return t;
}

牛顿迭代法

描述

牛顿迭代公式: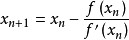 称为r的n+1次近似值.

开平方

1
2
3
4
5
6
7
8

double sqrt(double x) {
  double eps = 1e-12;
  double t = x;
  while (abs(t - x / t) > eps * t) {
    t = (t + x / t) / 2.0;
  }
  return t;
}

double sqrt2(double x) {
  double eps = 1e-12;
  double t = x;
  double lastt;
  do {
    lastt = t;
    t = (t + x / t) / 2.0;
  } while (abs(t-lastt) > eps);
  return t;
}

杨辉三角

最大公约数

欧几里得算法(辗转相除法)

欧几里德算法又称辗转相除法，是指用于计算两个正整数a，b的最大公约数。应用领域有数学和计算机两个方面。
计算公式gcd(a,b) = gcd(b,a mod b)。

1
2
3
4
5
6

int gcd(int a，int b)
{
    if (a < b)
        std::swap(a, b);
    return b == 0 ? a : gcd(b, a % b);
}

Stein算法

Stein算法由J. Stein于1961年提出，这个方法也是计算两个数的最大公约数。和欧几里德算法不同的是，Stein算法只有整数的移位和加减法，这对于程序设计者是一个福音。

gcd(a,a) = a，也就是一个数和他自身的公约数是其自身
gcd(ka,kb) = k gcd(a,b），也就是最大公约数运算和倍乘运算可以交换，特殊的,当k=2时，说明两个偶数的最大公约数必然能被2整除

质数(素数)

质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。

素数的判定

判定给定的正整数n,是否是素数

1
2
3
4
5
6
7
8

bool isPrime(int n) {
  for (int i = 2; i <= sqrt(n); i++) {
    if (n%i == 0) {
      return false;
    }
  }
  return true;
}

素数因子(质数因子)

三角函数

圆周率

描述

圆周率的值的求法

1.割圆术

圆周率的几何意义

导数

设函数y=f（x）在点x0的某个邻域内有定义，当自变量x在x0处有增量Δx，相应地函数取得增量Δy=f（x0+Δx）-f（x0）；如果Δy与Δx之比当Δx→0时极限存在，则称函数y=f（x）在点x0处可导，并称这个极限为函数y=f（x）在点x0处的导数。马克-to-win @ 马克java社区： 所以说：函数y=f（x）在x0点的导数f’（x0）的几何意义：表示函数曲线在点P0（x0,f（x0））处的切线的斜率（导数的几何意义是该函数曲线在这一点上的切线斜率）。