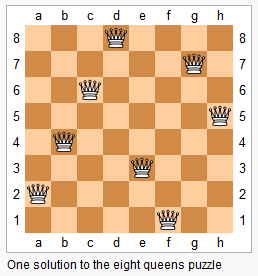
leetcode.51.N皇后
Wormholes
Wormholes
问题描述
Farmer John’s hobby of conducting high-energy physics experiments on weekends has backfired, causing N wormholes (2 <= N <= 12, N even) to materialize on his farm, each located at a distinct point on the 2D map of his farm (the x,y coordinates are both integers).
According to his calculations, Farmer John knows that his wormholes will form N/2 connected pairs. For example, if wormholes A and B are connected as a pair, then any object entering wormhole A will exit wormhole B moving in the same direction, and any object entering wormhole B will similarly exit from wormhole A moving in the same direction. This can have rather unpleasant consequences.
For example, suppose there are two paired wormholes A at (1,1) and B at (3,1), and that Bessie the cow starts from position (2,1) moving in the +x direction. Bessie will enter wormhole B [at (3,1)], exit from A [at (1,1)], then enter B again, and so on, getting trapped in an infinite cycle!
| . . . .
| A > B . Bessie will travel to B then
+ . . . . A then across to B again
Farmer John knows the exact location of each wormhole on his farm. He knows that Bessie the cow always walks in the +x direction, although he does not remember where Bessie is currently located.
Please help Farmer John count the number of distinct pairings of the wormholes such that Bessie could possibly get trapped in an infinite cycle if she starts from an unlucky position. FJ doesn’t know which wormhole pairs with any other wormhole, so \fBfind all the possibilities (i.e., all the different ways that N wormholes could be paired such that Bessie can, in some way, get in a cycle\fP). Note that a loop with a smaller number of wormholes might contribute a number of different sets of pairings to the total count as those wormholes that are not in the loop are paired in many different ways.
Milking Cows
Milking Cows
问题描述
Milking Cows
Three farmers rise at 5 am each morning and head for the barn to milk three cows. The first farmer begins milking his cow at time 300 (measured in seconds after 5 am) and ends at time 1000. The second farmer begins at time 700 and ends at time 1200. The third farmer begins at time 1500 and ends at time 2100. The longest continuous time during which at least one farmer was milking a cow was 900 seconds (from 300 to 1200). The longest time no milking was done, between the beginning and the ending of all milking, was 300 seconds (1500 minus 1200).
Your job is to write a program that will examine a list of beginning and ending times for N (1 <= N <= 5000) farmers milking N cows and compute (in seconds):
- The longest time interval at least one cow was milked.
- The longest time interval (after milking starts) during which no cows were being milked.
农民挤奶牛,每个农民有各自的挤奶时间段
求至少有一名农民在挤奶的最长连续时间段
求没有一个农民在挤奶的最长时间间隔
Broken Necklace
leetcode.850.矩形面积
矩形面积
问题描述
我们给出了一个(轴对齐的)矩形列表 rectangles 。 对于 rectangle[i] = [x1, y1, x2, y2],其中(x1,y1)是矩形 i 左下角的坐标,(x2,y2)是该矩形右上角的坐标。
找出平面中所有矩形叠加覆盖后的总面积。 由于答案可能太大,请返回它对 10 ^ 9 + 7 取模的结果。
示例 1:
输入:[[0,0,2,2],[1,0,2,3],[1,0,3,1]]
输出:6
示例 2:
输入:[[0,0,1000000000,1000000000]]
输出:49
解释:答案是 10^18 对 (10^9 + 7) 取模的结果, 即 (10^9)^2 → (-7)^2 = 49 。
提示:
- 1 <= rectangles.length <= 200
- rectanges[i].length = 4
- 0 <= rectangles[i][j] <= 10^9
- 矩形叠加覆盖后的总面积不会超越 2^63 - 1 ,这意味着可以用一个 64 位有符号整数来保存面积结果。
空间压缩
cmake
cmake
跨平台的安装(编译)工具
CMake是一个跨平台的安装(编译)工具,可以用简单的语句来描述所有平台的安装(编译过程)。他能够输出各种各样的makefile或者project文件,能测试编译器所支持的C++特性,类似UNIX下的automake。只是 CMake 的组态档取名为 CMakeLists.txt。Cmake 并不直接建构出最终的软件,而是产生标准的建构档(如 Unix 的 Makefile 或 Windows Visual C++ 的 projects/workspaces),然后再依一般的建构方式使用。这使得熟悉某个集成开发环境(IDE)的开发者可以用标准的方式建构他的软件,这种可以使用各平台的原生建构系统的能力是 CMake 和 SCons 等其他类似系统的区别之处。
单项目构建
基础
1 | cmake_minimum_required(VERSION 3.3.0) |
模快组织
文件目录结构
头文件和源文件分离
leetcode.10.正则表达式匹配
leetcode.43.字符串相乘
字符串相乘
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
十进制错位相乘
思路分析
代码实现
1 | class Solution { |
BM算法
BM算法
1.The bad character rule
1 | void badCharHeuristic( string str, int size, |
2.The good suffix rule
1 | // preprocessing for strong good suffix rule |