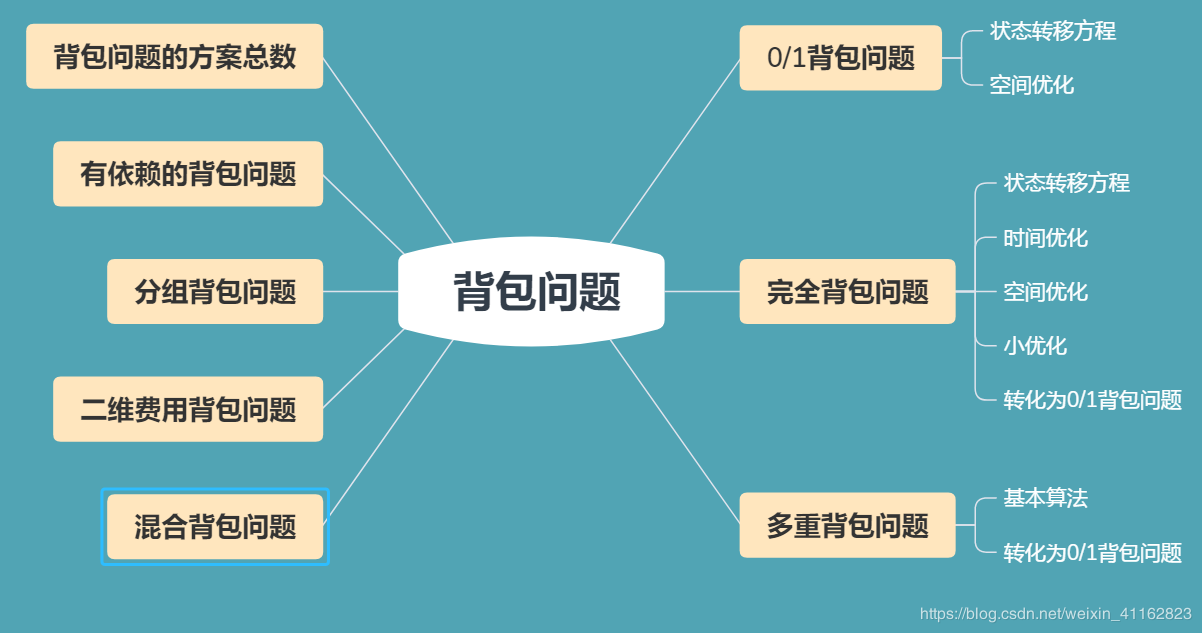
背包问题(Knapsack problem)
背包问题指这样一类问题,题意往往可以抽象成:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。
维基百科
部分背包问题
问题描述
部分背包问题和0/1背包问题的区别就是:部分背包问题中的单个物品,可以取一部分装入背包。而0/1背包问题则是要么全部拿走,要么一无所有
Subset Sum Problem
问题描述
If for each item the profit and weight are equal, we get the subset sum problem
Given a set of N (N≤40) integers each of them is at most 1012 determine the largest sum subset having sum less than or equal S (S≤1018)