lambda表达式

sort函数使用lambda表达式

priority_queue使用lambda表达式

求数组中第K个最大元素 最小堆

1
2
3
4
5
6
7
8
9
10
11
12
13

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        int n = nums.size();
        auto cmp=[](int a,int b){return a>b;};
        priority_queue<int,vector<int>,decltype(cmp)> pq(cmp);
        for(int i = 0; i < n; i ++){
            if(pq.size()<k){pq.push(nums[i]);}
            else if(pq.top()<nums[i]){pq.pop();pq.push(nums[i]);}
        }
        return pq.top();
    }
};

求数组中第K大的元素 最大堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

class KthLargest {
private:
    int k;
    priority_queue<int,vector<int>,greater<int>> pq;
public:
    KthLargest(int k, vector<int>& nums) {
        this->k = k;
        int n = nums.size();
        for(int i = 0; i < n; i ++){
            if(pq.size()<k){pq.push(nums[i]);}
            else if(pq.top()<nums[i]){pq.pop();pq.push(nums[i]);}
        }
    }

    int add(int val) {
        if(pq.size()<this->k){pq.push(val);}
        else if(pq.top()<val){pq.pop();pq.push(val);}
        return pq.top();
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class KthLargest {
    struct cmp{
        bool operator ()(int &x,int &y){
            return x>y;
        }
    };
private:
    int k;
    priority_queue<int,vector<int>,KthLargest::cmp> pq;
public:
    KthLargest(int k, vector<int>& nums) {
        this->k = k;
        int n = nums.size();
        for(int i = 0; i < n; i ++){
            if(pq.size()<k){pq.push(nums[i]);}
            else if(pq.top()<nums[i]){pq.pop();pq.push(nums[i]);}
        }
    }

    int add(int val) {
        if(pq.size()<this->k){pq.push(val);}
        else if(pq.top()<val){pq.pop();pq.push(val);}
        return pq.top();
    }
};

大文件排序

多线程归并排序

前向星

什么是前向星？
一种数据结构，以储存边的方式来存储图。构造方法如下：读入每条边的信息，将边存放在数组中，把数组中的边按照起点顺序排序(可以使用基数排序，如下面例程)，前向星就构造完了。通常用在点的数目太多，或两点之间有多条弧的时候。一般在别的数据结构不能使用的时候才考虑用前向星。除了不能直接用起点终点定位以外，前向星几乎是完美的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

int m,cnt=0,head[MAXN];
//另外还有一个数组head[],它是用来表示以i为起点的第一条边存储的位置,实际上你会发现这里的第一条边存储的位置其实
//在以i为起点的所有边的最后输入的那个编号

struct edge{
    int to;//其中edge[i].to表示第i条边的终点
    int nxt;//edge[i].next表示与第i条边同起点的下一条边的存储位置
    int dis;//edge[i].dis为边权值
}e[MAXE];

void add(int u,int v,int dis){//加边
    e[cnt].dis=dis;
    e[cnt].to=v;
    e[cnt].nxt=head[u];
    head[u]=cnt++;
}

最短路径

描述

所谓最短路径问题是指：如果从图中某一顶点（源点）到达另一顶点（终点）的路径可能不止一条，如何找到一条路径使得沿此路径上各边的权值总和（称为路径长度）达到最小。

Dijkstra算法(迪杰斯特拉算法)

1)算法思想：设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

(1) 初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为”起点s到该顶点的距离”[例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为∞]。
(2) 从U中选出”距离最短的顶点k”，并将顶点k加入到S中；同时，从U中移除顶点k。
(3) 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。
(4) 重复步骤(2)和(3)，直到遍历完所有顶点。

Floyd-Warshall算法

路径矩阵
通过一个图的权值矩阵求出它的每两点间的最短路径矩阵。
从图的带权邻接矩阵A=[a(i,j)] n×n开始，递归地进行n次更新，即由矩阵D(0)=A，按一个公式，构造出矩阵D(1)；又用同样地公式由D(1)构造出D(2)；……；最后又用同样的公式由D(n-1)构造出矩阵D(n)。矩阵D(n)的i行j列元素便是i号顶点到j号顶点的最短路径长度，称D(n)为图的距离矩阵，同时还可引入一个后继节点矩阵path来记录两点间的最短路径。
采用松弛技术（松弛操作），对在i和j之间的所有其他点进行一次松弛。所以时间复杂度为O(n^3);

Dijkstra算法(迪杰斯特拉算法)

A*算法

Bellman-ford算法

SPFA

Floyd-Warshall算法

K短路问题

POJ.2449

leetcode.1044. 最长重复子串

给出一个字符串 S，考虑其所有重复子串（S 的连续子串，出现两次或多次，可能会有重叠）。

返回任何具有最长可能长度的重复子串。（如果 S 不含重复子串，那么答案为 “”。）

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/longest-duplicate-substring
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

希尔排序

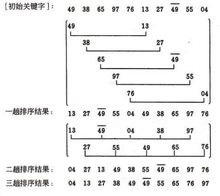
原始数组        49 33 45 97 76 13 27 49 55 04
增量为5,第一组  13 33 45 97 76 49 27 49 55 04
增量为5,第二组  13 27 45 97 76 49 33 49 55 04    
增量为5,第三组  13 27 45 97 76 49 33 49 55 04
增量为5,第四组  13 27 45 55 76 49 33 49 97 04
增量为5,第五组  13 27 45 55 04 49 33 49 97 76

增量为2,第一组  04 27 13 55 33 49 45 49 97 76
增量为2,第二组  04 27 13 49 33 49 45 55 97 76

增量为1,第一组  04 13 27 33 45 49 49 55 76 97
排序数组        04 13 27 33 45 49 49 55 76 97

八叉树

AStar

F = G + H

• G = 从起点A，沿着产生的路径，移动到网格上指定方格的移动耗费。
• H = 从网格上那个方格移动到终点B的预估移动耗费。这经常被称为启发式的，可能会让你有点迷惑。这样叫的原因是因为它只是个猜测。我们没办法事先知道路径的长度，因为路上可能存在各种障碍(墙，水，等等)。虽然本文只提供了一种计算H的方法，但是你可以在网上找到很多其他的方法。

1，把起始格添加到开启列表。

2，重复如下的工作：
a) 寻找开启列表中F值最低的格子。我们称它为当前格。
b) 把它切换到关闭列表。
c) 对相邻的8格中的每一个？

• 如果它不可通过或者已经在关闭列表中，略过它。反之如下。
• 如果它不在开启列表中，把它添加进去。把当前格作为这一格的父节点。记录这一格的F,G,和H值。
• 如果它已经在开启列表中，用G值为参考检查新的路径是否更好。更低的G值意味着更好的路径。如果是这样，就把这一格的父节点改成当前格，并且重新计算这一格的G和F值。如果你保持你的开启列表按F值排序，改变之后你可能需要重新对开启列表排序。

d) 停止，当你

• 把目标格添加进了关闭列表(注解)，这时候路径被找到，或者
• 没有找到目标格，开启列表已经空了。这时候，路径不存在。

3.保存路径。从目标格开始，沿着每一格的父节点移动直到回到起始格。这就是你的路径。

位图